1.二叉树
每个根节点拥有的子节点数量<=2
/**
二叉树的遍历有三种方式 (简记:把根放哪)
(1)前序遍历:根-左-右。
(2)中序遍历:左-根-右。
(3)后序遍历:左-右-根。
*/
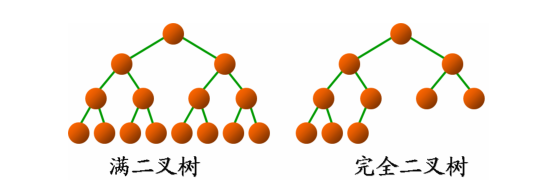
1.1满二叉树
/**
每一层级的节点数都在满额:
例如:第一层1 第二层2 第三层4 第五层8
总结:深度为k ,节点总合满足:2^k-1
总结:深度为k ,那么那一层的节点数为:2^(k-1)
*/
1.2完全二叉树
/**
完全二叉树:若设二叉树的深度为h,除第 h 层外,其它各层 (1~(h-1)层) 的结点数都达到最大个数,第h层所有的结点都连续集中在最左边,这就是完全二叉树。
//
注:完全二叉树是效率很高的数据结构,堆是一种完全二叉树或者近似完全二叉树,所以效率极高,像十分常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化,二叉排序树的效率也要借助平衡性来提高,而平衡性基于完全二叉树。
*/
2.平衡二叉树
/**
平衡二叉树:任一节点的左右子节点高度差都不超过1
//
平衡二叉树定义:平衡二叉树(Balanced Binary Tree),且具有以下性质:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用算法有红黑树、AVL树等。在平衡二叉搜索树中,我们可以看到,其高度一般都良好地维持在O(log2n),大大降低了操作的时间复杂度。
*/
2.1 AVL树
/**
AVL树就是 平衡树+二叉排序树,是以二叉排序树为基准,而且还满足平衡树的性质
//
用来解决一种极端情况的搜索,也就是二叉排序树 成了链表形式
*/
2.2 红黑树
/**
## 红黑树:
1.有标识为记录节点颜色,每个节点不是红就是黑
2.根节点是黑色的
3.任一节点到每个叶子节点,所经过的黑节点相同
4.红色节点的子节点 全部为黑色
5.他也算是AVL树,满足排序二叉树 和 平衡二叉树的 特点,他用来解决AVL 树,只适合查找,不适合频繁插入和删除等操作的弱势点
*/
3.二叉排序树
/**
二叉排序树:又称二叉查找树,二叉搜索树,和二分查找算法是一回事
1) 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2) 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
3) 左、右子树也分别为二叉排序树;
4) 中序遍历可得到从小到大的有序队列
*/

二叉排序树的特点
/**
上图就是一个二叉排序树
1.首先给了一个无序数列 int a[]=[5,3,4,1,7,8,2,6,0,9]
2.构建二叉排序树实质上是就是给他排序 ,int a[]=[0,1,2,3,4,5,6,7,8,9],当然构建排序二叉树很复杂,暂时不管
3.都知道啊 如果选5是根节点 左变所有节点都小于他,右边的都大于他,每个节点都是这样
4.那么我们现在目标就是找到9
步骤:a.首先从根节点开始(5),9>5,说明目标在右边,继续向下
b.再次找到(7),9>7,说明目标在右边,继续向下
c.再次找到(8),9>8,说明目标在右边,继续向下
d.找到9
//
原理 :二分查找法: 现有一组排序后的数组 arr[0,1,2,3,4,5,6,7,8,9]
目的:我们要找到9
第一次:找中间的arr[10/2]=arr[5]=5 <9 说明在5的右边 现在arr队列就成了arr[6,7,8,9]
第二次:找中间的arr[5/2]=arr[2]=8 8<9 说明在5的右边 现在arr队列就成了
arr[9]
第三次:找中间的arr[1/2]=arr[0]=9 找到了
*/
4.B树
5.B+树
6.B*树
B树为多路排序树,未完待续…